引言

想象这样的情形：水厂（图中的消防栓）通过流向、容量各不相同的水管供水到你所在的小区（图中的水桶），每次供水最多可以供多少呢？如果想切断到你所在小区的供水，我们最少该切断哪几根水管呢（如果切断成本与水管容量成正比）？

图源自https://brilliant.org/wiki/max-flow-min-cut-algorithm/

其实这就是图论中的最大流-最小割问题，本文用“水流”与“水管”类比，先讨论最大流问题，然后再说明最大流与最小割的特殊关系，我们还将讨论一些实际中会使用的相关算法及其实现。

直觉

每次供水量的最大值显然取决于传输路径中各根水管容量的最小值（类似木桶效应），不然当通过那根水管时，水管有可能会破裂。因此我们可以很快地想出这样的方法：每次寻找一条从出发点到目的地的可行路径，累加每条路径中水管容量的最小值，最后便是供水量的最大值。（注意：这并不完全正确）

我们可以找几个简单的例子试一试：

这只有一条路径，而其路径中最小值为2，那么我们每次供水量的最大值就是2，这显然是正确的。

再来看一个复杂些的例子：

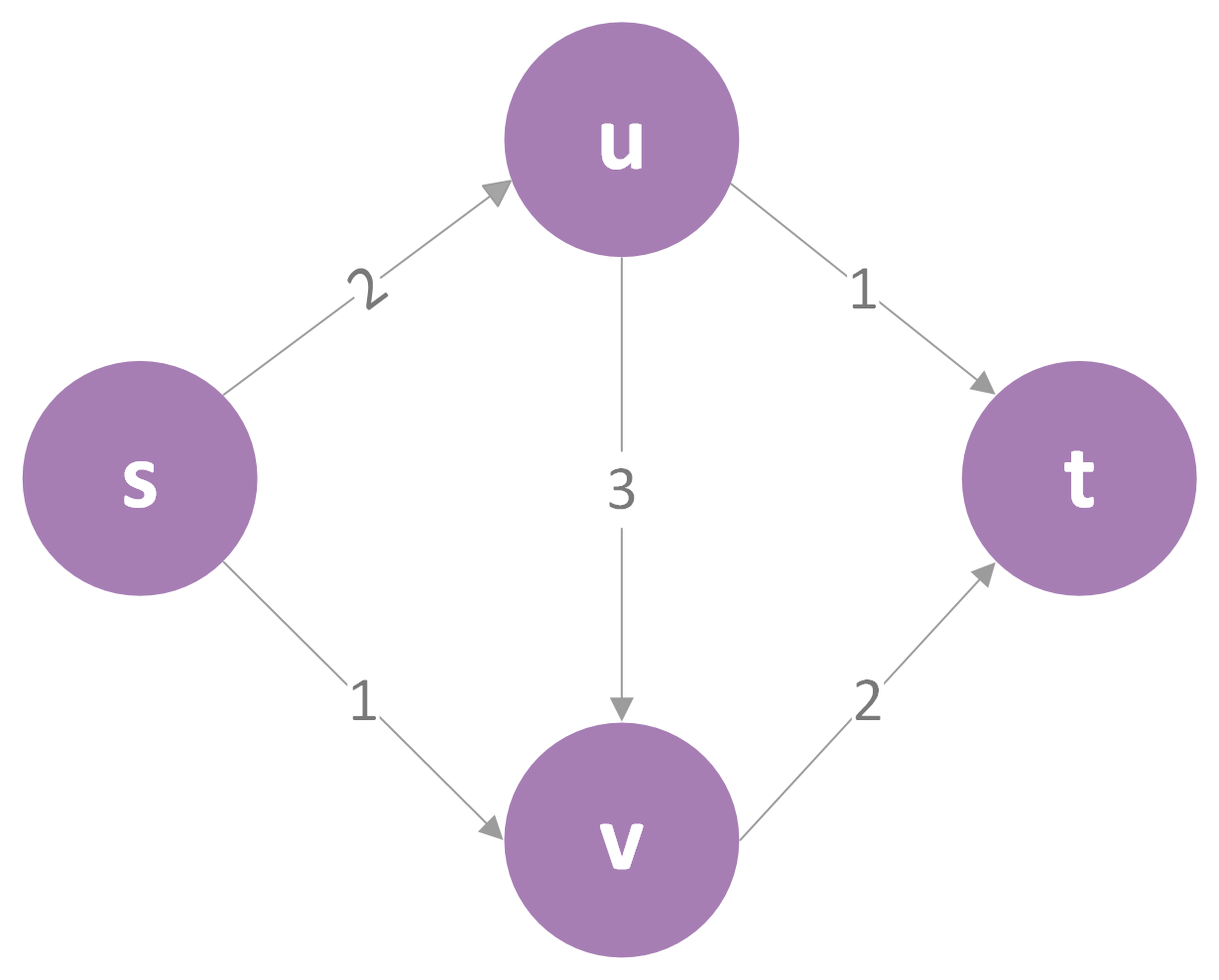
假如我们先找到的是s->u->v->t这一路径，那么其中最小值即为2，更新供水量为2，而后该图就变成了这样:

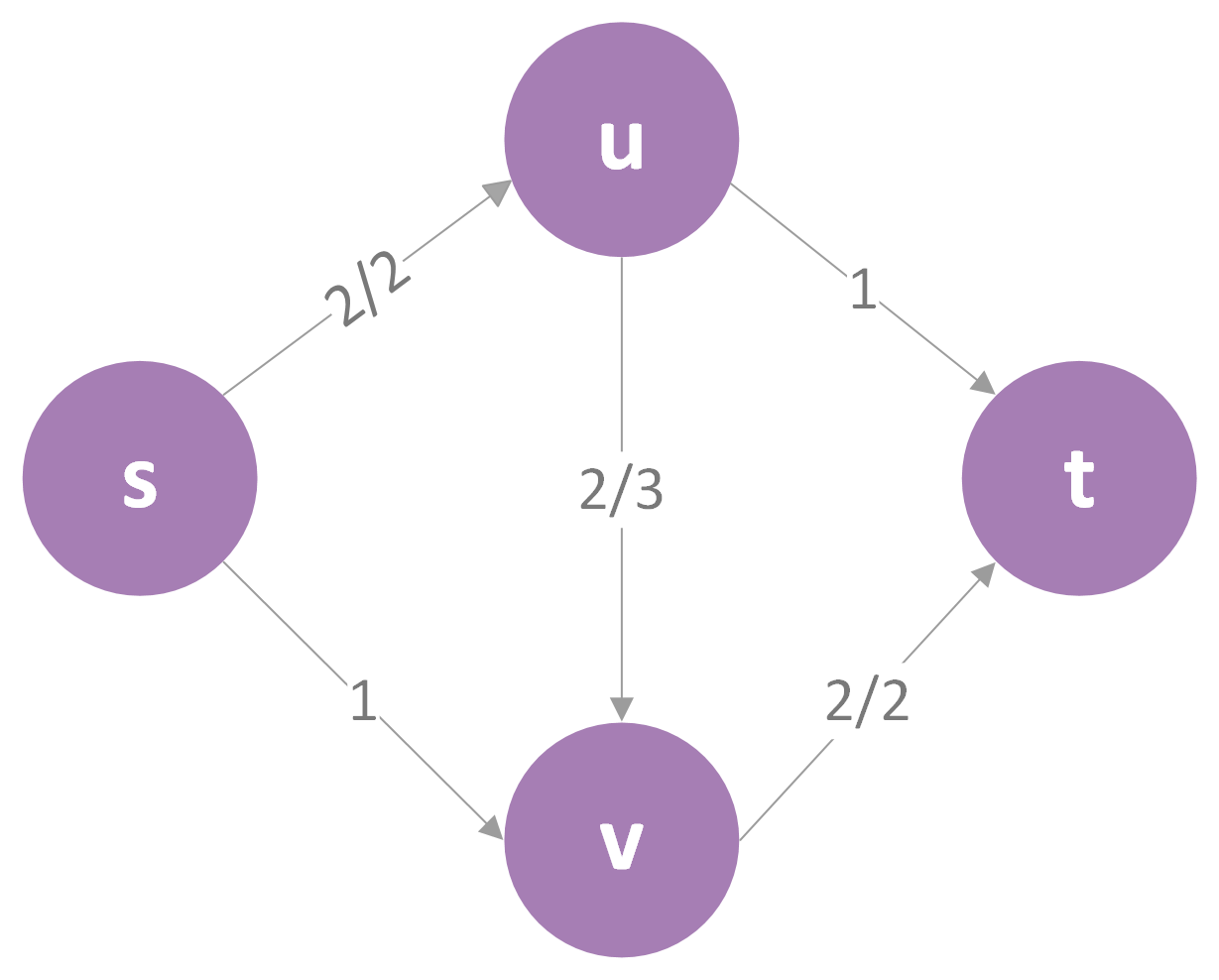
这里我们定义x/y表示容量最大值为y，我们已经用了x。由更新后的图，我们可以发现，已经没有可行的路径了，所以最后得出的供水量最大值即为2。但这是正确的吗？如果你仔细观察，你会发现，其实供水量的最大值应该是3，上方流量为2的水流一个走s->u->t，一个走s->u->v->t，下方流量为1的水流走s->v->t，如下图所示：

由此可见，我们单纯地寻找路径然后叠加不一定能得到正确的最大流，因为我们在流向选择时很可能是做出了错误的决定，比如上个例子，我们流量为2的水流本应分流但我们没有，这时我们就需要残留网络（residual graph）来让我们可以撤销（undo）错误的决定。

残留网络（residual graph）

残留网络是解决问题的关键，也是最让人疑惑的地方，在这里我尽量用易懂的语言和图示来说明。

个人认为，残留网络的关键思想在于：为了可以撤销（undo）先前的流向决定，我们就需要减小原先路径的可流量并对应地增加反向路径的可流量。为什么还可以增加反向路径的可流量？因为在残留网络中，反向路径的流量并不是说明我们真的可以倒着流，而只是说明我们可以撤销（undo）先前在这条路径过来的这么多流量，让它流向其他路径。下面我们再用上一个例子来讲解利用残留网络是如何成功地找到最大流的。

在第一次寻找路径时，我们找到了s->u->v->t，其最小值为2，那么我们就将路径中各根水管的可流量（最初就是容量）减2，对应反向路径加2。

我们在这给个图（注意：为了清晰美观，对于残留网络中的权值，我们不再使用x/y这种形式，而换用可流量表示，且可流量为0的边直接删去）：

这张图是怎么来的呢？我们按边来一一解释。在路径s->u->v->t中的每条边可流量都减2，那么s->u的可流量便从2降为0，我们将其删去，并加上可流量为2的反向路径，这一反向路径是说明，我们之前在这通入了2的水流，那么以后我们最多可以撤销2的水流。u->v的可流量从3降为1，反向路径也是2，最后v->t与s->u情形一样。

我们再尝试寻找一条路径，可以找到s->v->u->t，其最小值为1，那么我们就将路径中各根水管的可流量减1，对应反向路径加1，得到下面这个图：

在这里着重说下v<->u路径，本来是u->v可流量为1，可撤回流量为2，现在我们撤回了流量为1的u->v水流并让其走u->t路径，所以u->v可流量变为2，可撤回流量为1，即最初我们到u的2水流，现在1走u->v，1走u->t。

再次寻找路径，发现没有可行的路径，结束。因此最终最大流为2+1=3。

Ford-Fulkerson方法

其实前面我们求解最大流的方法就是Ford-Fulkerson方法。这一方法只需重复以下步骤：

寻找一条从出发点到目的地的可行路径，称为增广路径（argumenting path），没有则结束
找出该路径中权值的最小值
用这一最小值更新该路径中的前向边与反向边
将这一最小值累加到max_flow上（max_flow初始为0）

最终得到的max_flow就是最大流。

Ford-Fulkerson为什么是称为方法而不是算法呢？因为它并没有指定如何寻找一条增广路径。一般而言有两种实现方法:

DFS，总时间复杂度为$O(EC)$，$E$为图的边数，$C$为出发点$s$邻接边的权值之和$C:=\sum\limits_{e\,leaving\,s}C_e$。
BFS，总时间复杂度为$O(VE^2)$，$V$为图的顶点个数，是较优的算法，称为Edmonds-Karp算法。

为什么BFS优于DFS？

我们可以看这样一个例子，显然最大流为20000：

DFS寻找路径是不稳定的，我们在这里讨论最坏情况。假如我们第一次寻找到的路径为s->u->v->t，那么更新max_flow为1，得到下图：

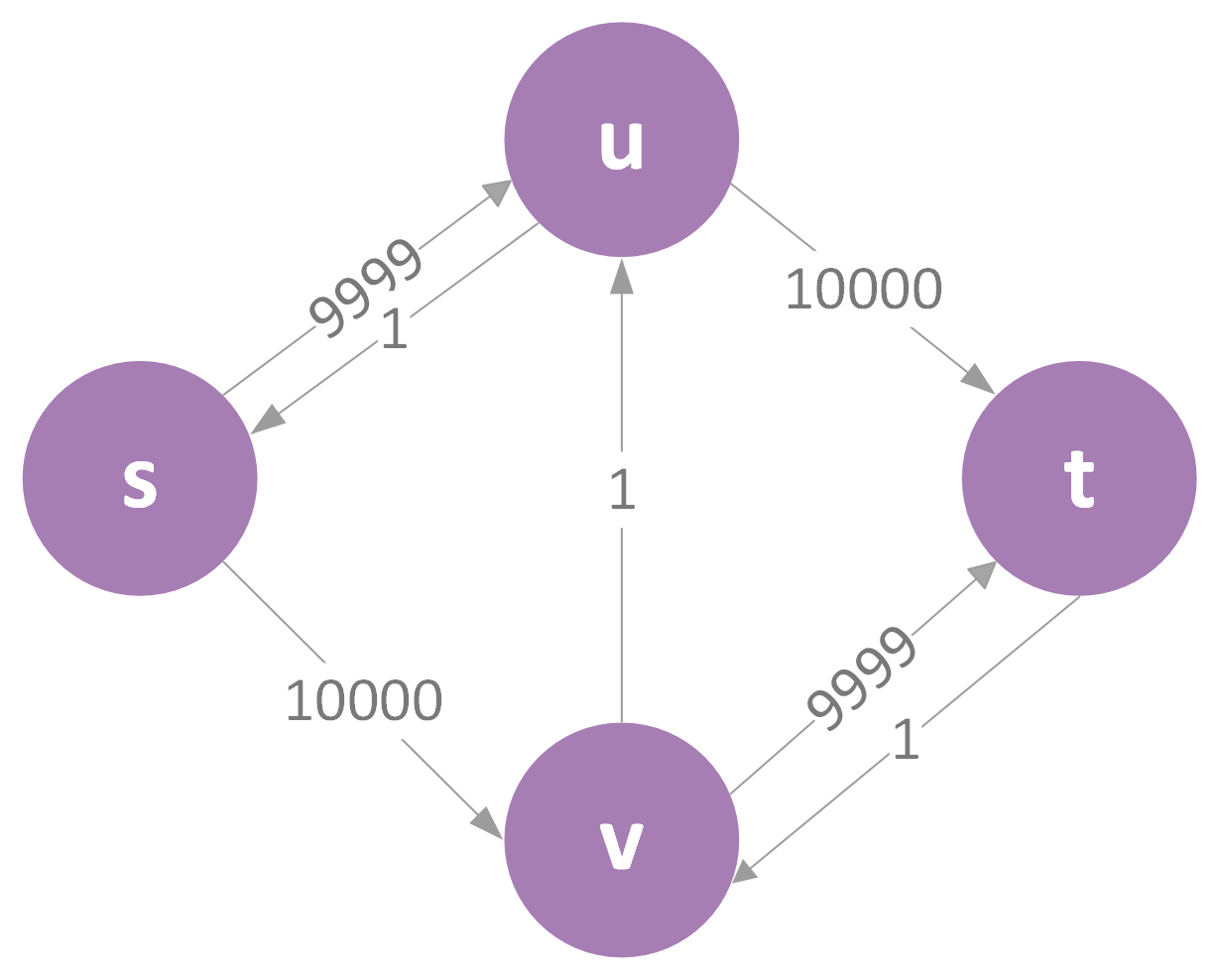
此时如果再寻找到的路径为s->v->u->t，那么更新max_flow为2，又会得到下图:

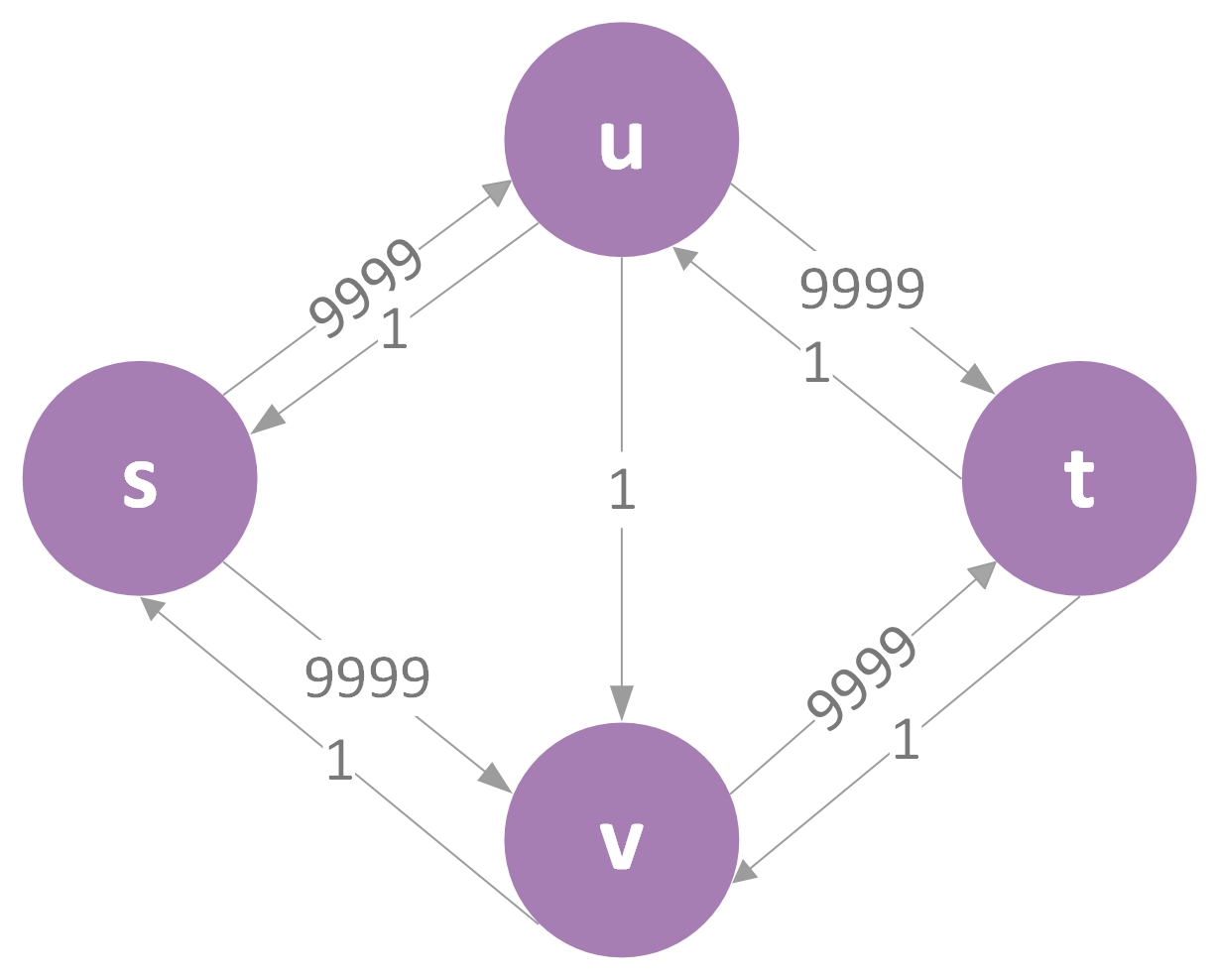
我们可以发现，若如此反复，我们需要20000次迭代寻找路径，才能达到最大流。这就是使用DFS的弊端，由于寻找路径的不稳定，当出发点邻接边权值之和很大时，效率有可能极低。

而如果我们使用BFS，将流图当成无权图，那么我们每次都可以确定地找到最短路径，这样时间复杂度也就仅与顶点数、边数有关了，没有潜在的低效率风险。

方法实现

在这里我们给出伪代码（若需要多语言版本的实现，可参见这里）：

rGraph = graph   // 用原图初始化残留网络
max_flow = 0
while finding a path p from s to t in rGraph with DFS or BFS {
    min_edge = min{e(u, v) for all e（u, v) in p};
    for each edge e(u, v) in p {
        rGraph[u][v] -= min_edge;   // 更新前向边
        rGraph[v][u] += min_edge;   // 更新后向边
    }
    max_flow += min_edge;
}
return max_flow;

最大流与最小割的关系

最大流最小割定理：最大流=最小割。为了彻底理解这一定理，我们这里不得不涉及一些数学证明。

什么是割？简单来说，割就是将一个图切割为互不相连的子图。最小割是s-t割，是将一个图分为两个子集$S$和$T$，它们满足以下关系：

$S \cup T = V$
$S \cap T = \varnothing$
$s \in S \, and \, t \in T$

我们还需要知道什么是s-t割的容量，即从$S$集合指向$T$集合的边的权值之和（$T$集合指向$S$集合的不算），可以表示为

$c(S,T)=\sum\limits_{u \in S} \sum\limits_{v \in T}e(u,v)$

最小割的目的就是让s-t割的容量最小。

对于一个s-t流，多少是从$S$集合真正流到$T$集合的呢？显然是它从$S$集合流到$T$集合的量减去从$T$集合流到$S$集合的量，即

$\begin{equation} \begin{aligned} f(S,T) &= \sum\limits_{u \in S} \sum\limits_{v \in T} f(u,v) - \sum\limits_{v \in T} \sum\limits_{u \in S} f(v,u) \\ &= f^{out}(S) - f^{in}(S) \end{aligned} \end{equation}$

有了以上这些定义的铺垫，我们可以很容易地写出以下关系式：

$\begin{equation} \begin{aligned} f(S,T) &= f^{out}(S) - f^{in}(S) \\ &\leq f^{out}(S) \\ &= \sum\limits_{e \, leaving \, S}f(e) \\ &\leq \sum\limits_{e\, leaving\, s} c(e) \\ &= C(S,T) \end{aligned} \end{equation}$

也就是当没有从$T$集合流入$S$集合的流量时，s-t流达到了最大值，而一条边的流量最大就是等于其容量，那么我们就得到了最大流=最小割。