动态连通性问题

现实世界中，人际关系时常变化，如何快速判断两个人是否是朋友关系？路径不断增删，如何快速判断两个地点是否互通？这些都是动态连通性问题，现在已经有很好的算法来解决他们，即并查集算法。

问题建模

在这一问题中，显然最关键的就是物体和连通。对于各个物体，我们可以用整数表示，如N个物体，使用0～N-1表示；对于连通，学过离散数学的朋友应该能很自然地想到连通性是一种等价关系（满足自反性、对称性和传递性），这一关系将物体分为一个个等价类（连通集）。

算法解决

简单的想法：quick-find

对于N个物体，显然可以使用一个一维的数组来储存，而对于连通性的判断，我们可以对一个连通集维护一个值，即当两个节点存储的值相等时，认为它们在同一连通集中。

public boolean connected(int p, int q) {
    return id[p] == id[q];
}

public void union(int p, int q) {
    int pid = id[p];
    int qid = id[q];
    for (int i = 0; i < id.length; i++) {
        if (id[i] == pid)
            id[i] = qid;
    }
}

这样判断连通性仅需O(1)，但合并操作却需要O(N)，我们需要对合并操作做一定的优化。

优化1：quick-union

quick-find的合并操作较慢是由于需要遍历数组来寻找在同一连通集的元素并加以修改，而quick-union为了解决这一问题换了一种思路：将N个物体看作森林，每一个连通集是一棵树，这样我们只需判断两个节点是否在一颗树上，即根节点是否相等，就可以知道它们是不是在同一连通集中。

令id[p]为节点p的父节点，若id[p] == p，则p为根节点：

private int root(int i) {
    while (i != id[i])
        i = id[i];
    return i;
}

public boolean connected(int p, int q) {
    return root(p) == root(q);
}

public void union(int p, int q) {
    int i = root(p);
    int j = root(q);
    id[i] = j;
}

这样一来，在已求出两节点的根节点时，合并操作是O(1)的。但是如果表示连通集的树退化成链表，求根节点的操作还会是O(N)的，因此我们需要寻找办法来降低树的高度。

优化2：weighted quick-union

方法一就是对树赋权值（表示大小），在每次合并操作中，将小树的根连接到大树的根上，以此达到平衡树高度的目的，如下图所示。

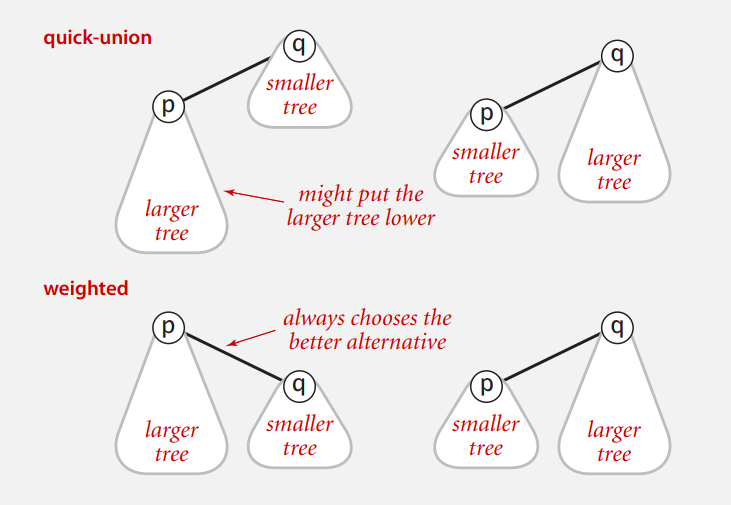
实现的方法也很简单，只需像维护id数组一样维护一个表示连通集大小的sz数组即可（这里只给出union的实现，其他基本不变）：

public void union(int p, int q) {
 	int i  = root(p);
    int j = root(q);
    if (i == j) 
        return;
    if (sz[i] < sz[j]) {
        id[i] = j;
        sz[j] += sz[i];
    } else {
        id[j] = i;
        sz[i] += sz[j];
    }
}

经过这样的加权平衡操作，我们求根节点的操作仅需O(lg N)了，证明如下：

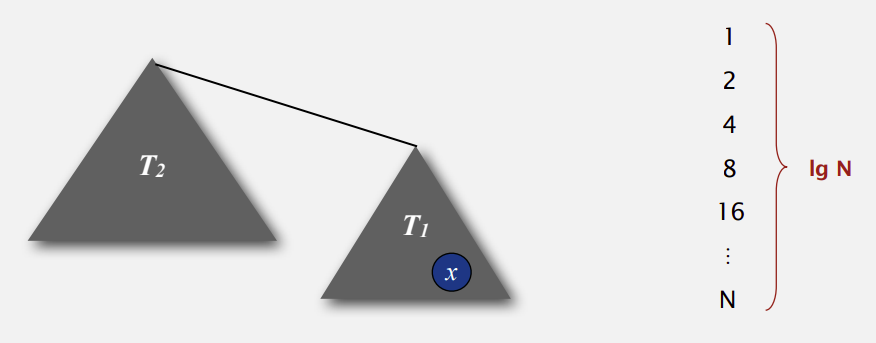
对于一个节点x，它所在的深度仅会在它所在的连通集作为子树连到另一连通集上时加一，如下图，x的深度仅会在它所在的连通集T1作为子树连到T2上时会加一。在合并操作后，T1和T2会作为一个新的连通集T继续以后的操作，它的大小至少是原来T1大小的两倍。总共有N个节点，翻倍的次数最多为lg N次，因此求根节点操作为O(lg N)。

优化3：path compression

在求根节点的过程中，我们可以顺便进行路径的压缩以达到降低树高度的目的。由于我们之前定义过：“若id[p] == p，则p为根节点”，因此我们可以让路径上的每个点指向其祖父节点，即id[p] = id[id[p]]，这样可以使寻根的路径减半，也不会影响根节点。在不断的合并操作下，树的高度可以趋近于1。

private int root(int i) {
    while (i != id[i]) {
        id[i] = id[id[i]];
        i = id[i];
    }
    return i;
}

综合运用weighted quick-union和path compression的情况下，摊还分析表示判断连通性与合并操作都为常数时间。

Assignment: Percolation

这周的大作业是判断一个正方形渗透模型的动态连通性，代码见这里。在这主要说明下完成作业的两个关键点：

二维转一维。对于这样一个N x N的正方形渗透模型，其本质是判断第一行与最后一行是否有元素在一个连通集中，因此也就是一个并查集问题。我们需要将二维的坐标对应到一维的、大小为N x N + 2的数组坐标上。（2是用于减少计算量的上下两个虚拟节点）
解决backwash。完成任务的朋友可能会发现，测试input10.txt时显示的图像与参考答案不符，与最后一行相连的open的块集合均变为了蓝色，其实这就是所谓的backwash。这是因为渗透时，上面的虚拟节点与下面的虚拟节点在同一连通集中，最后一行与下面的虚拟节点也在同一连通集中，这就导致与最后一行相连的open块集合就会直接与上面的虚拟节点在同一连通集中，因此对这些块isFull函数都判断为true，它们也就显示为蓝色了。解决方法有两个：
1. 去掉下面的虚拟节点。这样最后一行就不会与下面的虚拟节点在同一连通集中，模型渗透时也就不会直接与上面的虚拟节点在同一连通集了。但这样判断模型是否渗透时就需要上面的虚拟节点与最后一行的元素进行一一判断，时间复杂度为O(N)。
2. 增加一个并查集。新的并查集与原来的并查集差别只在于新的并查集没有虚拟节点。在平时的操作中，需要对两个并查集都进行操作，而判断模型是否渗透时，只判断新的并查集。这一方法就是用空间换时间了，时间复杂度仅为O(1)。