Mergesort

归并排序是一种基于分治思想的稳定排序算法，其时间复杂度为$O(nlogn)$。

我们在此不详细讨论算法本身的设计与实现，而注重于证明其时间复杂度的正确性。

若我们用比较的次数来表示时间的复杂度，那么对于长度为$N$的数组，我们可写出如下不等式：

$$C(N) \leq C(N/2) + C(N/2) + N$$

其中$C(N)$是整个数组的比较次数，最后的$N$是归并操作的比较次数。

为了便于求解，我们仅讨论$N = 2^k, k = 0,1,…$的情况（结论适用于所有$N$），则式子转化为

$$D(N) = 2*D(N/2) + N, D(1) = 0$$

对于上式我们可以画出递归树来帮助理解过程：

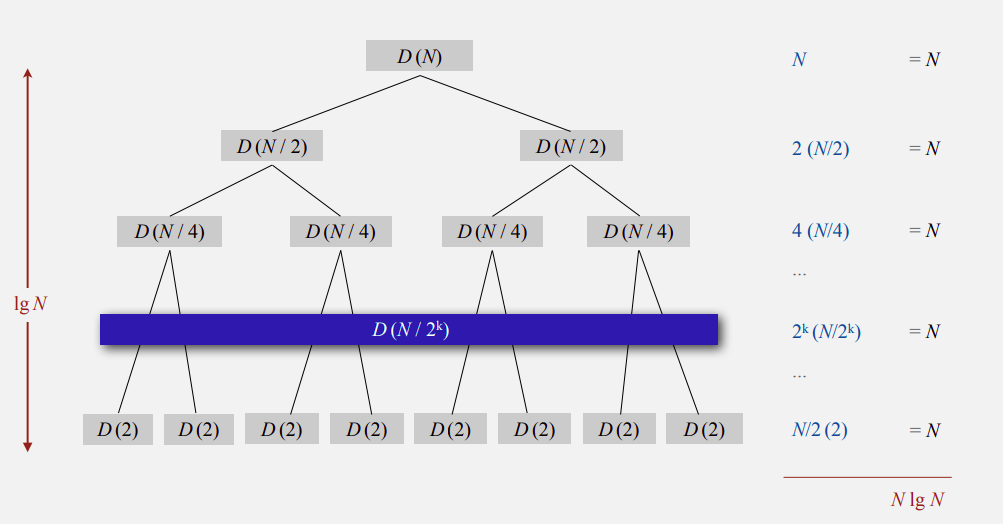
算法从$N$个数一直处理到两个数，每次对半分开处理，所以递归深度为$log_2N$，树的高度也就为$log_2N$，每次递归处理最终归并的比较次数都是$N$次，所以最终比较次数也就是$Nlog_2N$次，则该算法的时间复杂度也就是$O(NlogN)$。

Quicksort

快速排序是一种基于分治思想的不稳定排序算法，其平均时间复杂度为$O(NlogN)$，最差情况为$O(N^2)$。

同样，我们在这里也只是证明算法的时间复杂度，而不讨论该算法的设计与实现。

一般情况

对于不重复元素的数组(distinct numbers)，划分的比较次数恒为$N+1$，且我们假定划分的各种情况概率均等，即划分出的两个子数组元素个数为0与$N-1$、1与$N-2$…的概率都相等。则我们可以得出以下等式：

$$C_N = (N+1) + (\frac{C_0+C_{N-1}}{N}) + (\frac{C_1+C_{N-2}}{N}) + ...+ (\frac{C_{N-1}+C_{0}}{N})$$

方程两边同乘$N$，得

$$NC_N = N(N+1)+2(C_0+C_1+...+C_{N-1})$$

令

$$NC_N - (N-1)C_{N-1}$$

再方程两边同除$N(N+1)$，得

$$\begin{aligned} \frac{C_N}{N+1} &= \frac{C_{N-1}}{N}+\frac{2}{N+1} \\ &= \frac{C_{N-2}}{N-1} + \frac{2}{N} + \frac{2}{N+1} \\ &=... \\ &=\frac{2}{3}+\frac{2}{4}+\frac{2}{5}+...+\frac{2}{N+1} \end{aligned}$$

则

$$\begin{aligned} C_N &= 2(N+1)(\frac{1}{3}+\frac{1}{4}+...+\frac{1}{N+1}) \\ &\sim 2(N+1)\int_{3}^{N+1}\frac{1}{x}dx \end{aligned}$$

最终可得

$$C_N \sim 2(N+1)lnN \approx 1.39NlogN$$

所以平均时间复杂度为$O(NlogN)$。

最差情况

最差情况是数组已经完全有序（顺序或逆序），此时总的比较次数为

$$N+(N-1)+(N-2)+...+1 \sim \frac{1}{2}N^2$$

基于比较的排序算法的最优时间复杂度

任何基于比较的排序算法在最坏情况下都至少需要大约$NlogN$次比较。

证明：

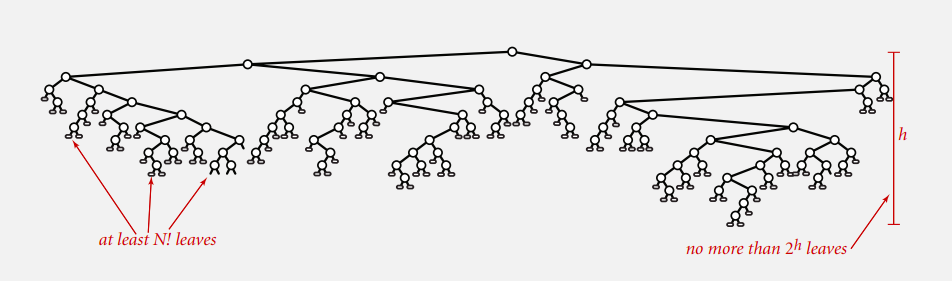
最坏情况即需遍历所有的可能排列，共$N!$种排列情况。对于决策树而言，也就是至少有$N!$个叶节点。比较次数就是树的高度$h$，则树最少有$2^h$个叶节点。

综上，我们可以得出以下不等式：

$$2^h \ge num \space of \space leaves \ge N! \\ h \ge lg(N!) \sim NlogN$$

所以，至少需要$NlogN$次比较次数。

Assignment: Collinear Points

代码见这里。在这主要说明下完成作业的几个关键点：

• 该数据类型需要是不可变的(immutable)，即无论中间有多少不同的操作，内部数据都不应有变化。
• 避免重复。在我们根据斜率排序然后加入满足条件的线时，可能会加入前面已经加入过的线。为了避免这一点，我们可以对满足条件的线加一个条件判断，若该线的出发点（即当前点）是整条线上坐标最小的点，才加入，否则跳过。