问题描述

1. 旅行商问题（TSP）：从一点出发遍历其余点各一次再回到该点，要求总路径最短。
2. 最可靠路径问题：图中的任一条边都有其可靠的概率，求任意两点间的最可靠路径。

问题建模

旅行商问题

若图中有$n$个点，我们可将它们编号为$0,…,n-1$（本文讨论都默认0为起点）,构造对应的邻接矩阵c_nxn，令x_nxn为0-1矩阵，若x_ij为1，则点$i$到点$j$属于当前选择路径的一部分，反之不属于。那么我们就可以很容易写出如下目标函数

$$min \sum_{i=1}^{n}\sum_{j=1}^{n}c_{ij}x_{ij}$$

显然，在此题中一条合法的路径应该是类似下方这样的回路。

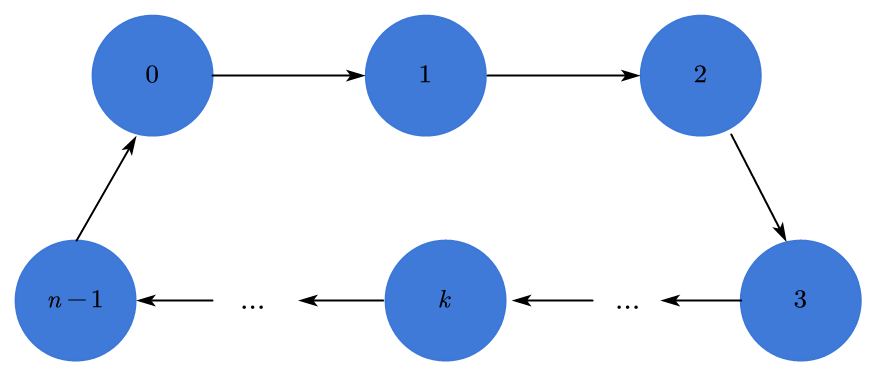
这样的一条回路，其中各点的入度、出度都应为0。所以我们可以写出以下两条约束条件

$$\begin{equation} s.t. \left\{\begin{aligned} \sum_{i=1}^{n}x_{ij} = 1, j = 1,...,n \\ \sum_{j=1}^{n}x_{ij} = 1, i = 1,...,n \end{aligned} \right. \end{equation}$$

但是仅仅满足这两个条件的路径可能并不是合法路径，因为它可能是多条回路的并集而非一个回路。如下图所示。

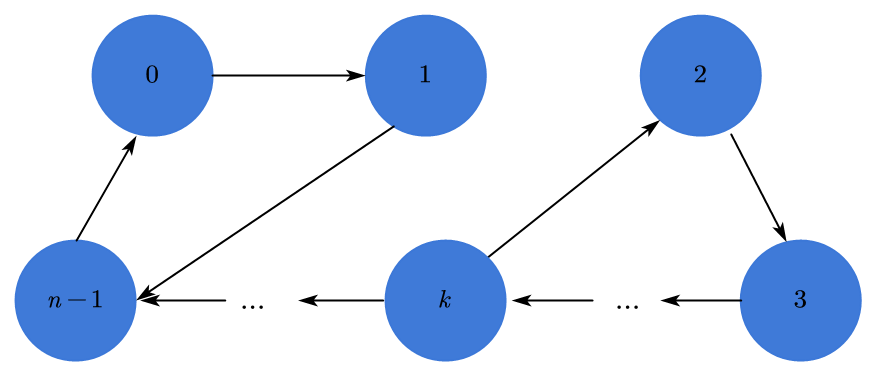
因此我们还需要第三个约束条件

$$u_i - u_j + nx_{ij} \leq n - 1， 1< i \neq j < n$$

其中$u_i$表示编号为$i$的点在当前选择路径的序号（该点为非起点，在本文中即非0）。加上这一约束条件，我们就可以确定合法路径，证明如下。

约束三的证明

1. 必要条件

   

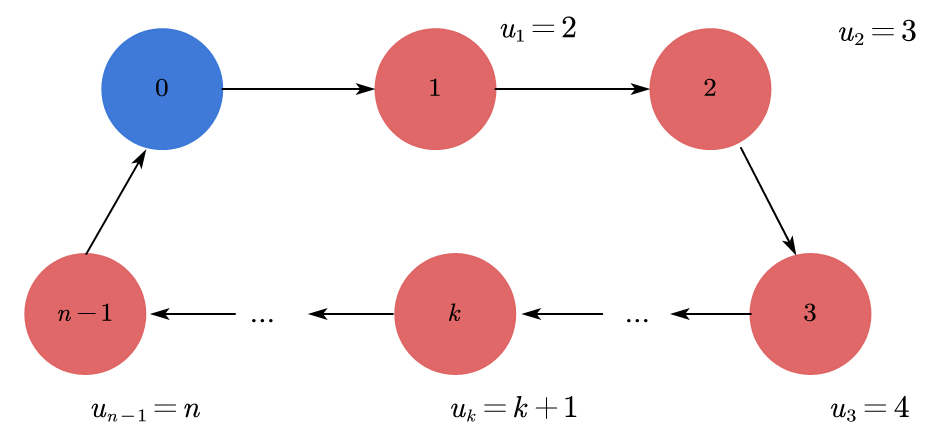
（注意：起点0并没有对应的$u$值，它不参与计算。）

对于一条合法路径，根据$x_{ij}$的取值，我们有两种情况要讨论

• 若$x_{ij}=1$，即点$i$与点$j$相邻，则$|u_i-u_j| \leq 1$，所以$u_i-u_j+n \times 1 \leq n-1$，成立。
• 若$x_{ij}=0$，即点$i$与点$j$不相邻，而$max \space u_i=n$，$min \space u_j = 2$，那么$max \space (u_i-u_j) + n \times 0=n-2 < n-1$，也成立。

因此，加上约束三后的约束条件是确定合法路径的必要条件。

1. 充分条件

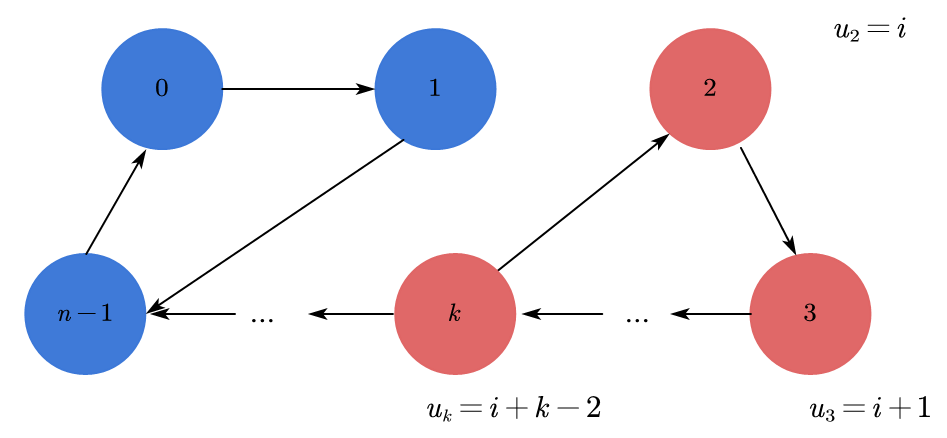
我们使用反证法。满足前两个约束的非法路径肯定是多条回路的并集，我们选择不包含起点的某个回路来讨论。比如我们选中上图的右回路，我们假定其中各点对应$u$值如图所示（其实对应$u$值具体为多少并不重要，只要是连续的即可）。我们可以写出以下式子：

$$\begin{aligned} \left\{\begin{aligned} u_2 - u_3 + n \times 1 \leq n - 1 \\ u_3 - u_4 + n \times 1 \leq n - 1 \\ u_4 - u_2 + n \times 1 \leq n - 1 \end{aligned} \right. \end{aligned}$$

全部式子加和，可得

$$k \times n \leq k \times (n - 1)$$

显然，该式不成立。因此，加上约束三后的约束条件是确定合法路径的充分条件。

综上，加上约束三后的约束条件是确定合法路径的充分必要条件。

最可靠路径问题

对一个图G< V, E >，其任意一条边$e_i \in E$都有其可靠的概率$p_i$，任意两点的最可靠路径我们的目标函数大致可以写成

$$max \sum p_i$$

这个最大值其实并不好求，我们可以将其转化为最短路径问题。

令各边长为$l_i = log_2 \frac{1}{p_i}$，$p_i$越大，$\frac{1}{p_i}$就越小，由于$log$函数是单调递增的函数，那么$l_i$也就越小。

即，我们的目标函数变为

$$\begin{aligned} max \sum p_i &= min \space log_2\frac{1}{p_i} \\ &= min \space -log_2p_i \end{aligned}$$

这就完成了从最可靠路径问题到最短路径问题的转化。求解最短路径的方法多样，就不在此多加探讨了。